Phyllotaxis

In botany, phyllotaxis or phyllotaxy is the arrangement of leaves on a plant stem (from Ancient Greek phýllon "leaf" and táxis "arrangement"). Phyllotactic spirals form a distinctive class of patterns in nature.

The Algorithm for Phyllotaxis:

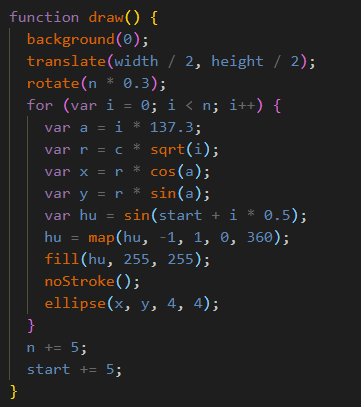
Consider 'n' to be the number of dots in the phyllotaxis pattern,'c' be the scaling factor for the dots, and 'r = c * sqrt(n)' be the radius of the nth dot. The standard angle for the the nth dot in the pattern is a = (137.5 * n). The polar coordinates,radius and angle, are then converted to Cartesian coordinates where x = r * cos(a) and y = r * sin(a). As the number of dots increases, the angle is adjusted with it, and a dot is produced at the corresponding Cartesian coordinates.

The following animation in p5.js visualizes the Phyllotaxis pattern.

The code for the above visualization is given below.



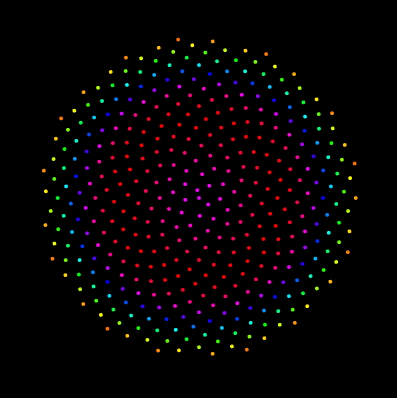
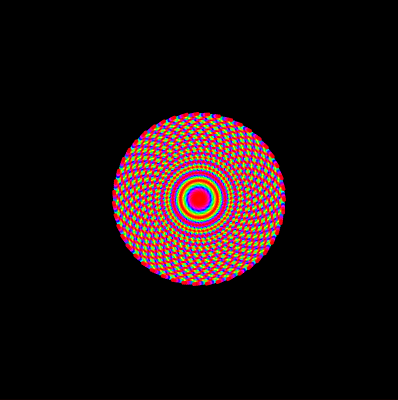
The following are different patterns drawn with some values for different scaling factor 'c' and angle 'a':

c=3 a=137.5

c=8 a=137.5

c=3 a=137.2

c=1 a=137.9

To know more :

//en.wikipedia.org/wiki/Phyllotaxis

Discover more